Scientific notation is a powerful mathematical tool used to express very large or very small numbers in a simplified, yet precise manner. By converting numbers into a format that combines a coefficient and an exponent, scientific notation streamlines complex calculations across various fields such as physics, engineering, and computer science. Scientific notation not only helps in handling extreme values but also makes mathematical operations like multiplication, division, and powers more efficient. Understanding its application goes beyond basic mathematics; it is essential in scientific research, data analysis, and real-world problem-solving scenarios.
In this guide, we will explore the core concepts of scientific notation, its mathematical foundations, and how it is applied in practical situations.
What is Scientific Notation?
Scientific notation is a powerful mathematical tool that simplifies the representation of very large or very small numbers. It expresses numbers in the form of a×10ba×10b, where aa is a coefficient (the significand) and bb is an exponent indicating the power of ten. This format not only makes calculations more manageable but also enhances clarity in scientific and engineering contexts.
Components of Scientific Notation
In scientific notation, the significand aa must fall between 1 and 10, while the exponent bb can be positive (indicating large numbers) or negative (indicating small numbers).
Conversion to Scientific Notation
To convert a standard number into scientific notation, follow these steps:
- Move the decimal point in the number until you have a number between 1 and 10.
- Count how many places you moved the decimal point. This count becomes the exponent.
- If you move it to the left, the exponent is positive.
- If you move it to the right, the exponent is negative.

Performing Calculations in Scientific Notation
Addition and Subtraction:
When adding or subtracting numbers in scientific notation, ensure that the exponents are aligned. For example:
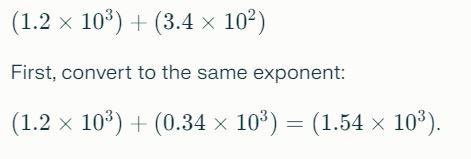
Multiplication
To multiply numbers in scientific notation, multiply the significands and add the exponents:
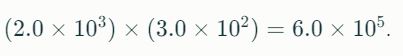
Division
For division, divide the significands and subtract the exponents:
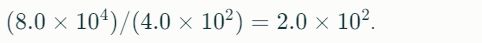
The rule for multiplying the numbers in scientific notation works in a way that coefficients are multiplied with the coefficients and later on powers are added. For example,
(a×10b)×(c×10d)=(a×c)×10(b+d)
For division, you need to divide the coefficients and subtract the powers.
(a×10b)/ (c×10d)=(a/c)×10 b-d
Practical Applications of Scientific Notation
Scientific notation is widely used across various fields such as science, engineering, and finance to handle extreme values efficiently. Many online calculators and software tools are available to assist with calculations involving scientific notation, making it easier for users to perform complex mathematical operations.
E Notation vs. Scientific Notation
E notation is an alternative format often used in computing (e.g., 1.23e41.23e4). While both formats serve similar purposes, scientific notation is more common in academic contexts.
Conclusion
Understanding scientific notation and its calculations is essential for anyone engaged in scientific or technical fields. By mastering this topic, you can simplify your work with large and small numbers, ensuring accuracy and clarity in your calculations. Practice converting numbers and performing operations in scientific notation to enhance your skills further!

Sheema Ahmed is a passionate writer and educator, specializing in crafting content tailored for individuals preparing for challenging exams such as CSS, SAT, and ACT. Born with a fervour for education, Sheema’s journey began at Hazara University, where she graduated with distinction, solidifying her commitment to academic excellence.
